自控中的一些概念

自控中的一些概念【持续更新】

阻尼值对应的响应

一个系统受初扰动后不再受外界激励，因受到阻力造成能量损失而位移峰值渐减的振动称为阻尼振动。系统的状态由阻尼比ζ来划分。不同系统中ζ的计算式不同，但意义一样。把ζ=0的情况称为无阻尼，即周期运动；把0<ζ<1的情况称为欠阻尼；把ζ>1的情况称为过阻尼；把ζ=1的情况称为临界阻尼，即阻尼的大小刚好使系统作非“周期”运动。 理想状态下，与欠阻尼况和过阻尼相比，在临界阻尼情况下，系统从运动趋近平衡所需的时间最短。

传递函数

传递函数描述只适用于线性定常系统
传递函数G(s)的拉氏反变换是脉冲响应g(t)。脉冲响应（也称脉冲过渡函数）是
系统在单位脉冲δ(t)瑜入时的输出响应，此时R(s)=L[δ(t)]=1.

三频段理论

1. 三频段理论有：低频、中频和高频段。
2. 低频段主要对应系统的稳态精度和响应速度(开环增益K，系统型别v)；
3. 中频段主要反映了系统的稳定性和动态性能(中频段对应了系统的幅值剪切频率和相频剪切频率，这分别对应了系统的幅值裕度h与相角裕度γ，同时相角裕度与剪切频率也决定了系统(尤其是高阶系统)的调节时间、峰值时间和超调量等参数，这反映了系统的动态性能；且中频段斜率最好是-20dB/dec
4. 高频段主要体现了系统的抗噪声能力，高频段的分贝斜率越大则抗噪声能力越好(高频噪声的幅值衰减越快)。
   注解：
   虽然对二阶系统而言，ts公式中仅与无阻尼自然震荡频率Wn有关，但是对高阶系统而言ts公式中与Wc截止频率成反比，因此中频段可看出系统的快速性，且相角裕度与高阶系统的谐振峰值Mr和超调量均成反比！ (高阶公式在胡寿松书P253)

   PID和滤波器的关系

   P 比例 I 积分 D 微分
   高通滤波器，又称低截止滤波器、低阻滤波器，允许高于某一截频的频率通过，而大大衰减较低频率的一种滤波器 。它去掉了信号中不必要的低频成分或者说去掉了低频干扰。
   有源高通滤波器：由无源元件(一般用R和C)和有源器件(如集成运算放大器）组成。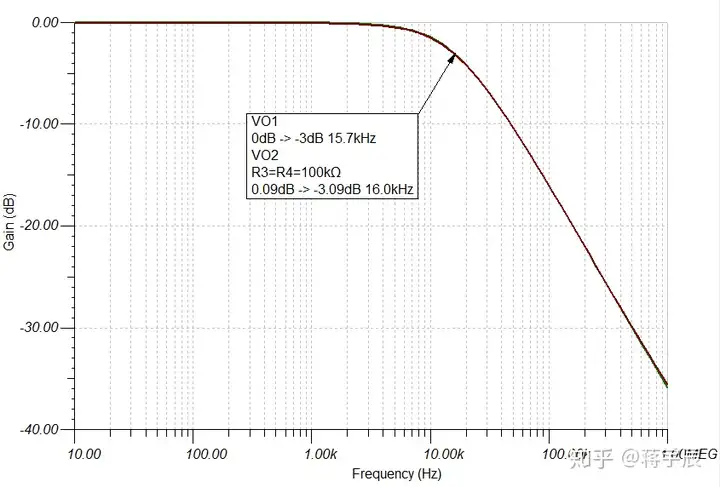
   
   
   
   可知低通滤波器相当于比例积分 高通滤波器相当于比例微分
   状态反馈未必能保持能观性，输出反馈可同时保持能观性